Tag Archives: Simulation

Why I use Panel/Multilevel Methods

Posted in ggplot2, Panel, R, Regression Modelling by

I don’t understand why any researcher would choose not to use panel/multilevel methods on panel/hierarchical data. Let’s take the following linear regression as an example:

y_{it} = \beta_{0} + \beta_{1}x_{it} + a_{i} + \epsilon_{it},

where a_{i} is a random effect for the i-th group. A pooled OLS regression model for the above is unbiased and consistent. However, it will be inefficient, unless a_{i}=0 for all i.

Let’s have a look at the consequences of this inefficiency using a simulation. I will simulate the following model:

y_{it} = 1 + 5 x_{it} + a_{i} + \epsilon_{it},

with a_{i} \sim N(0, 3) and \epsilon_{it} \sim N(0, 1). I will do this simulation and compare the following 4 estimators: pooled OLS, random effects (RE) AKA a multilevel model with a mixed effect intercept, a correlated random effects (CRE) model (include group mean as regressor as in Mundlak (1978)), and finally the regular fixed effects (FE) model. I am doing this in R, so the first model I will use the simple lm() function, the second and third lmer() from the lme4 package, and finally the excellent felm() function from the lfe package. These models will be tested under two conditions. First, we will assume that the random effects assumption holds, the regressor is uncorrelated with the random effect. After looking at this, we will then allow the random effect to correlate with the regressor x_{it}.

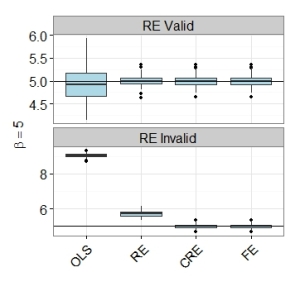
The graph below shows the importance of using panel methods over pooled OLS. It shows boxplots of the 100 simulated estimates. Even when the random effects assumption is violated, the random effects estimator (RE) is far superior to simple pooled OLS. Both the CRE and FE estimators perform well. Both have lowest root mean square errors, even though the model satisfies the random effects assumption. Please see my R code below.

remc

# clear ws
rm(list=ls())

# load packages
library(lme4)
library(plyr)
library(lfe)
library(reshape)
library(ggplot2)
# from this:

### set number of individuals
n = 200
# time periods
t = 5

### model is: y=beta0_{i} +beta1*x_{it} + e_{it}
### average intercept and slope
beta0 = 1.0
beta1 = 5.0

### set loop reps
loop = 100
### results to be entered
results1 = matrix(NA, nrow=loop, ncol=4)
results2 = matrix(NA, nrow=loop, ncol=4)

for(i in 1:loop){
  # basic data structure
  data = data.frame(t = rep(1:t,n),
                    n = sort(rep(1:n,t)))
  # random effect/intercept to add to each 
  rand = data.frame(n = 1:n,
                    a = rnorm(n,0,3))
  data = join(data, rand, match="first")
  # random error
  data$u = rnorm(nrow(data), 0, 1)
  # regressor x
  data$x = runif(nrow(data), 0, 1)
  # outcome y
  data$y = beta0 + beta1*data$x + data$a + data$u  
  # make factor for i-units
  data$n = as.character(data$n)
  # group i mean's for correlated random effects
  data$xn = ave(data$x, data$n, FUN=mean)
  # pooled OLS
  a1 = lm(y ~ x, data)
  # random effects
  a2 = lmer(y ~ x + (1|n), data)
  # correlated random effects
  a3 = lmer(y ~ x + xn + (1|n), data)
  # fixed effects
  a4 = felm(y ~ x | n, data)
  
  # gather results
  results1[i,] = c(coef(a1)[2],
                  coef(a2)$n[1,2],
                  coef(a3)$n[1,2],
                  coef(a4)[1])
  ### now let random effects assumption be false
  ### ie E[xa]!=0
  data$x = runif(nrow(data), 0, 1) + 0.2*data$a
  # the below is like above
  data$y = beta0 + beta1*data$x + data$a + data$u  
  data$n = as.character(data$n)
  data$xn = ave(data$x, data$n, FUN=mean)
  a1 = lm(y ~ x, data)
  a2 = lmer(y ~ x + (1|n), data)
  a3 = lmer(y ~ x + xn + (1|n), data)
  a4 = felm(y ~ x | n, data)
  
  results2[i,] = c(coef(a1)[2],
                  coef(a2)$n[1,2],
                  coef(a3)$n[1,2],
                  coef(a4)[1])  
}
# calculate rmse
apply(results1, 2, function(x) sqrt(mean((x-5)^2)))
apply(results2, 2, function(x) sqrt(mean((x-5)^2)))

# shape data and do ggplot
model.names = data.frame(X2 = c("1","2","3","4"),
                         estimator = c("OLS","RE","CRE","FE"))
res1 = melt(results1)
res1 = join(res1, model.names, match="first")
res2 = melt(results2)
res2 = join(res2, model.names, match="first")

res1$split = "RE Valid"
res2$split = "RE Invalid"
res1 = rbind(res1, res2)

res1$split = factor(res1$split, levels =  c("RE Valid", "RE Invalid"))
res1$estimator = factor(res1$estimator, levels =  c("OLS","RE","CRE","FE"))

number_ticks = function(n) {function(limits) pretty(limits, n)}

ggplot(res1, aes(estimator, value)) + 
  geom_boxplot(fill="lightblue") +
  #coord_flip() +
  facet_wrap( ~ split, nrow = 2, scales = "free_y") +
  geom_hline(yintercept = 5) +
  scale_x_discrete('') + 
  scale_y_continuous(bquote(beta==5), breaks=number_ticks(3)) + 
  theme_bw() + 
  theme(axis.text=element_text(size=16),
        axis.title=element_text(size=16),
        legend.title = element_blank(),
        legend.text = element_text(size=16),
        strip.text.x = element_text(size = 16),
        axis.text.x = element_text(angle = 45, hjust = 1))
ggsave("remc.pdf", width=8, height=6)

Monty Hall Meets Monte Carlo

Posted in Simulation by

In 1990, Parade magazine columnist Marilyn vos Savant caused a giant kerfuffle over an answer she gave to a question posed by a reader. The problem, as stated by the omnipotent Wikipedia, goes like this:

Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1 [but the door is not opened], and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?

Vos Savant’s answer was you should always switch. The probability of winning the star prize (a brand new Rover Vitesse Fastback) is 2/3 if you switch, and only 1/3 if you stick. However, this answer outraged many people, and 10,000 furious souls dabbed their quills in some ink and wrote strongly worded, and possibly impolite, letters to Vos Savant refuting her analysis. It was Vos Savant who would have the last laugh though, as her answer was indeed correct (LOL).

That people would get this puzzle wrong is understandable. I know I did the first time I was faced with it. The reason is deeply rooted in behavioural psychology. Humans are not good at dealing with conditional probabilities. If only Vos Savant’s irate readers knew how to use Bayes theorem, they could have saved themselves the ink and the emotional turmoil by deriving the analytic solution to the problem (although, on reflection, doing this would have also led to some ink usage).

What if you’re too lazy or unsure how to derive an analytic solution to the problem? Is there a way for you, you feckless badger? Why yes Kent, there is – use simulation. In the below, I have included some simple R code which simulates the problem. As you can see you get close enough to the Vos Savant’s correct answer.

The code below is an example of how it is possible to use simulation techniques to derive solutions when you do not want to, or are too stupid to do the mathematics. The beauty of computer simulation is that it can be used in much more complex settings where analytic solutions are not feasible. Extracting results via computer simulation is crucial in Bayesian statistical analysis, and also in frequentist calculations of model uncertainty like bootstrapping.

# clean
rm(list=ls())
# outcome matrix
cars <- matrix(NA,nrow=10000,ncol=2)
for(i in 1:10000){
   # initial choices
   choices <- 1:3
   cardoor <- sample(choices,1)
   goatdoor <- choices[-cardoor]
   contest <- sample(choices,1)
   choice2 <- c(contest,NA)
   choice2[2] <- ifelse(contest==cardoor,sample(goatdoor,1),cardoor)
   # the guy who sticks
   cars[i,1] <- ifelse(contest==cardoor,1,0)
   # the guy who changes
   cars[i,2] <- ifelse(choice2[choice2!=contest]==cardoor,1,0)
}

c(mean(cars[,1]),mean(cars[,2]))